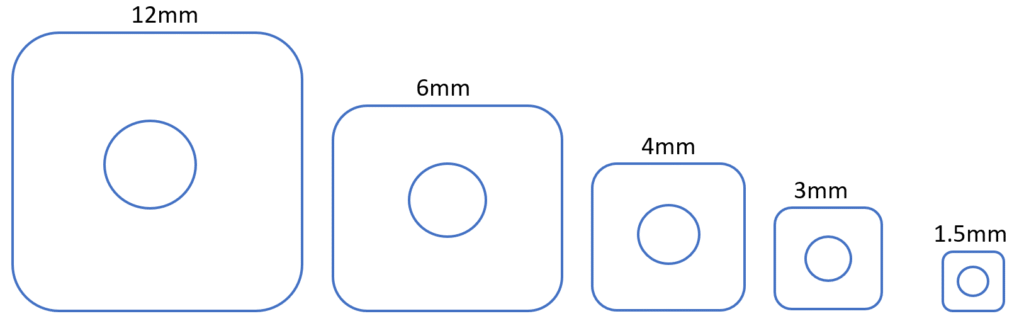
Ceramic resonator filters usually have high-Q resonating elements which gives the advantage of lower passband insertion loss. The resonators employ low loss dielectric materials and come in a different size depending on the Q-factor required. The various resonator sizes are shown below for reference.
Fractional bandwidth (FBW) is a common concept in filter design:
FBW=\frac{\text{Bandwidth}}{f_c}As shown in the equation above, fractional bandwidth refers to the ratio of the filter’s absolute bandwidth to its center frequency.
The fractional bandwidth plays a key role in determining the insertion loss of the filter. Consider two example filters, both with a center frequency of 1000 MHz. If one has a 50 MHz bandwidth, its fractional bandwidth is 5%. If another has a 100 MHz bandwidth, its fractional bandwidth will be 10%. In both cases, let us assume both filters use a 4th order design with the same ceramic resonator type — for instance, a 4 mm resonator with a quality factor of around 350. Let us assume both the filters are of 4th order and use the same type of ceramic resonator, say 4mm. The quality factor of individual resonators would be around 350.
Since the individual resonators have the same Q, one might expect similar insertion loss in both filters. However, this is not the case. Insertion loss and bandwidth are inversely related: the narrower 5% FBW filter will exhibit higher insertion loss than the 10% FBW filter.
The following plot and table compare the performance of both filters, highlighting the difference in insertion loss despite using identical resonator elements.
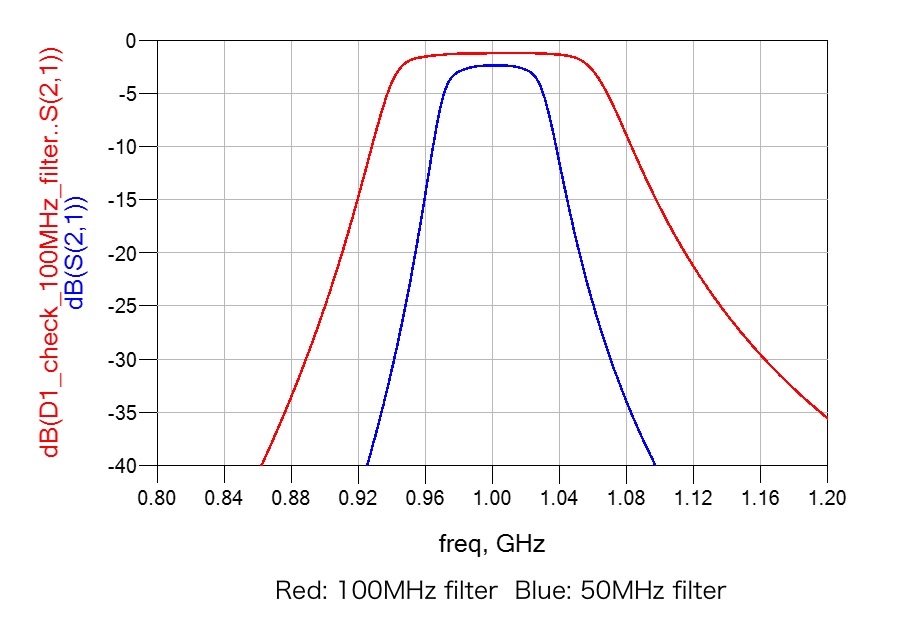
| Parameter | 50MHz Filter | 100MHz Filter |
| Lower cut-off, MHz | 975 | 950 |
| Upper cut-off, MHz | 1025 | 1050 |
| BW, MHz | 50 | 100 |
| Center Frequency, MHz | 1000 | 1000 |
| Fractional bandwidth | 5% | 10% |
| Order | 4 | 4 |
| Resonator size, mm | 4 | 4 |
| Mid-band insertion loss, dB | 0.93 | 0.53 |
In the above case, if we increase the Quality factor of the resonator used in the 50MHz filter, we can achieve the same insertion loss as the 100MHz filter. This higher Q can be obtained by using larger resonators, such as 6 mm or 12 mm types.
The size and fractional bandwidth as a function of Q-factor is plotted below. The below two graph are based on a 4th order design with a dielectric constant of 38.
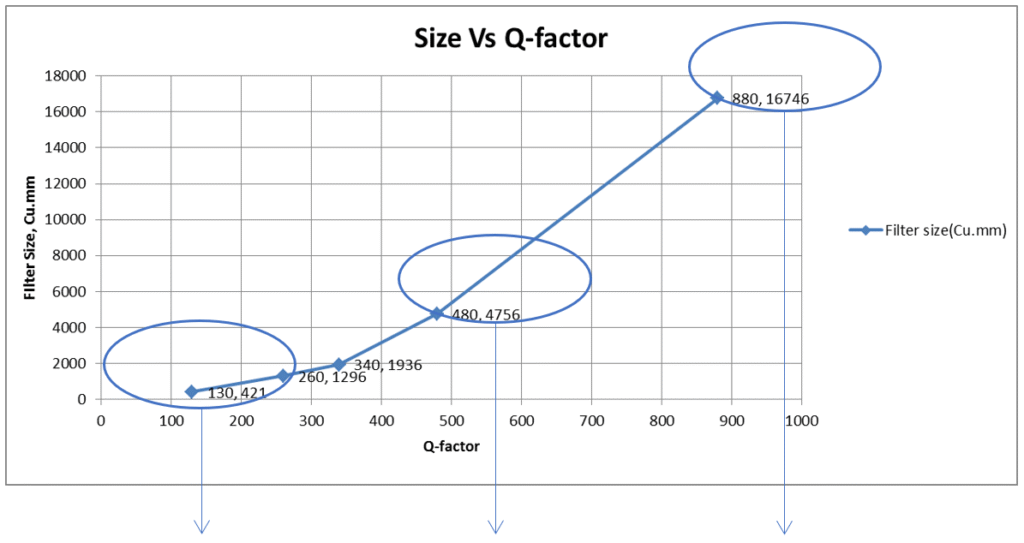
| This shows that the Q-factor is relatively low – around 130 – for a small resonator such as 1.5 mm in size. A typical 4th-order filter using this resonator would have a volume of approximately 421 mm³, with dimensions of 11.9 × 9.9 × 3.9 mm. | Here, the Q-factor is moderate – around 480 – for a medium-sized 6 mm resonator. A typical 4th-order filter in this case would have a volume of approximately 4756 mm³, with dimensions of 29 × 20 × 8.2 mm. | This configuration shows a high Q-factor of around 880, achieved with a larger 12 mm resonator. A typical 4th-order filter using this resonator would have a volume of approximately 16,746 mm³, with dimensions of 53 × 21 × 15 mm. |
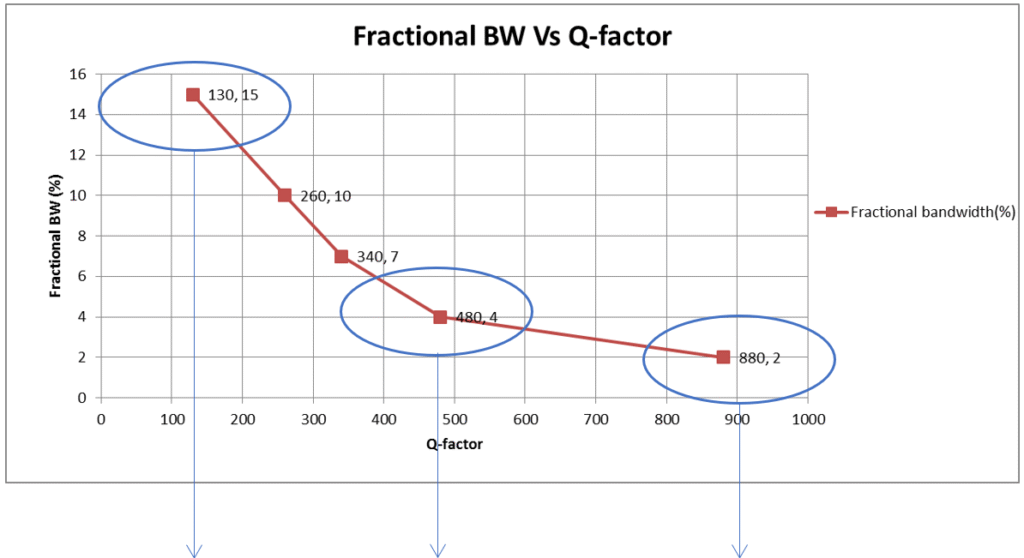
| This indicates a relatively low Q-factor – approximately 130 – for a compact 1.5 mm resonator. A corresponding 4th-order filter would have a volume of around 421 mm³, with dimensions of 11.9 × 9.9 × 3.9 mm. | This indicates a moderate Q-factor – approximately 480 – for a 6 mm resonator. For applications requiring a 4% bandwidth filter, the 6 mm resonator offers an optimal balance of compact form factor, cost, and performance. | This indicates a high Q-factor – approximately 880 – for a larger 12 mm resonator. For applications requiring a 2% bandwidth filter, the 12 mm resonator provides the most suitable form factor for achieving the desired performance, albeit at a higher cost. |
Conclusion
This analysis helps users identify the optimal trade-off between size, performance, and cost when selecting a coaxial ceramic resonator filter.
The 1.5 mm resonator offers the most compact form factor, while the 12 mm resonator delivers the highest performance. In some cases, filters using 12 mm resonators can approach the performance of cavity filters—at significantly reduced size and cost.
Ultimately, the ideal choice depends on the specific balance required between form factor, insertion loss, and price for the target application.
Mini-Circuits Resonators Link
https://www.minicircuits.com/WebStore/modelSearch.html?model=cbp&search=1
